In qualitative terms, power factor is a measure of the congruency of voltage and current ac waveforms imposed by a load on the power mains. Ignoring the relative phase of the two waveforms, the apparent power (S) is the simple product of the waveform amplitudes, S = V × I.
Limiting our focus for now to sinusoidal waveforms without significant harmonic content, we can separate the apparent power into its real (P) and reactive or quadrature (Q) components.
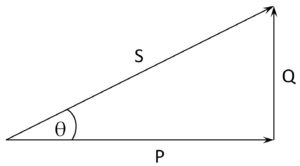
Apparent power S depicted as the combination of real and reactive parts.
The power factor (PF) is given simply as PF = cos(θ). Notably, resistive loads operate with unity power factor (θ = 0; S = P). These include ye olde incandescent lamps and non-inductive heating elements — nearly a redundancy — that comprised much of the original load to the first ac mains-power grids.
The most common cases of purely sinusoidal deviation from unity power factor derive from inductive components. For example, the no-load component of the apparent power a utility delivers to mains-connected transformers and inductive motors is reactive.
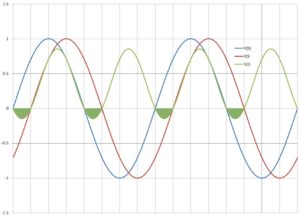
The reactive power—the integral of the filled-in regions of S(t) — simply sloshes back and forth between the utility energy source and the load, but it’s not a lossless process.
The power that does real work derives from the in-phase component. The reactive power — the integral of the filled-in regions of S(t) in the accompanying figure — simply sloshes back and forth between the utility energy source and the load, but that’s not a lossless process: Dissipation through the power distribution network derives primarily from I2R heating, which is real and independent of the relative phase of voltage and current waveforms. Also of concern to the utility, the total delivered current for loads operating at PF < 1 is greater than for unity PF loads by a factor of ![]()
.
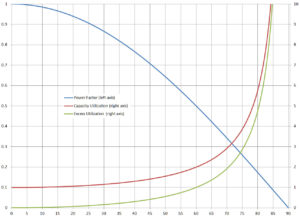
As the power factor decays further, the increase in excess utilization rapidly accelerates.
The reciprocal of the power factor, then, is a measure of source and grid current-capacity utilization for a given load. For loads that are close to unity — say 0.9 or better — the penalty for imperfect PF is modest, but as the power factor decays further, the increase in excess utilization rapidly accelerates.
From the customer’s perspective, you might wonder why any of this matters. After all, utility meters for all but large industrial customers measure only the real power. Large industrial sites are often equipped with two meters, one that measures real energy use and the other, often referred to as a VAR meter, which measures the power feed’s quadrature term. So if you’re not operating a large industrial site and not being billed for excess capacity utilization, why care?
Well, there are several reasons: Utilities base their rates, in part, on their real costs so, you’re paying for the losses. Excess utilization is essentially a preventable downgrade of infrastructure. Sooner than would otherwise be the case, rate payers or tax payers (same people, just different pockets) will be chipping in for capacity upgrades or living with over-extended grids and generation capacity. Does the phrase rolling blackouts sound familiar, California?
Excess utilization isn’t a problem that ends at the power meter: It extends to the premise wiring too. Although customer power meters only measure the in-phase component and, therefore, can’t detect excess capacity use, circuit breakers only monitor current, irrespective of relative phase. So within the premises, loads with poor power factor degrade branch capacity in the same way they degrade grid infrastructure, except branches start with already low current-carrying capability: 12-A continuous on a 15-A breaker at unity PF.






