A graduate student worked out the principles of using a planet’s mass to accelerate and adjust the voyage of spacecraft traversing our solar system; without it, the voyages of interplanetary probes would be impractically long.
If you follow the news about the various interplanetary probes launched by NASA, the European Space Agency (ESA) and others (and even if you don’t), you may have heard the term “gravity slingshot”, often along with the phrase “course correction.” The story of this slingshot effect, how it was quantified, and how it is used is fascinating, and even more so because it relies largely on the work of a single student with insight and determination.
Q: What is the fundamental issue with interplanetary and deep-space probes?
A: It’s simple: the high velocity which they must attain to leave orbit and escape Earth’s gravitational pull, called escape velocity (roughly 25,00 mph or 40,000 km/h), is still too low to complete a trip to even nearby planets in reasonable time; even a trip to nearby Mars would take many years. But achieving higher velocities from Earth-based launches for any object having useful size and mass would require too much fuel and weight in the launch vehicle.
Q: So why not just accelerate it after leaving Earth’s pull?
A: While that solution may seem simple — just give the spacecraft a boost after leaving Earth’s pull – the reality is that a spacecraft simply cannot carry enough fuel to do more than modest course corrections. Any fuel needed for further in-flight acceleration must also be boosted to reach escape velocity, so it’s a losing game, so to speak.
Q: Is the problem that simple?
A: Yes, the laws of physics are indisputable, starting with Newton’s laws and F = ma: Accelerating mass to high velocities is very costly in terms of fuel. Whether done as a single intense burst, a series of smaller bursts, or as a slow burn, the amount of fuel needed is about same to accelerate to a new, higher speed. Thus, additional in-flight, rocket-based propulsion is not an option, since the amount of fuel needed is prohibitive. Also note that any space destination is also a fast-moving target on a curved path that will really be at more distance than a simple “straight line” measurement implies, as there is no direct path for the journey between launch-point A and destination-point B.
Q: So, how do these missions each their goal?
A: They use a “free” technique called gravity assist, also referred to as a gravity “slingshot” for their propulsion. This is a rare case of getting “something for nothing” or having a “free lunch,”.
Q: What physics principle does it use?
A: It begins with Newton’s Law of Gravitational Attraction [ F = G (m1 × m2)/r2] and then leverages the gravitational attraction between the spacecraft and a nearby planet (and even the sun) to catapult or “slingshot” the vehicle as it travels, without the need for any ongoing rocket-based propulsion or fuel (References 1 and 2). This slingshot effect can be employed repeatedly with a single body in multiple circle-around passes, or used with more than one body in a series of slingshot events.
Q: It seems obvious enough, what’s the big deal? Who came up with idea?
A: The discovery of this technique is largely due to one person’s inspiration, insight, and extremely complex mathematical analysis. Prior to this revelation, there was real frustration that interplanetary missions would take so long that they would be impractical in many cases. Without the slingshot boost, a spacecraft could not reach its destination without traveling for many additional years, assuming it could reach it at all.
Q: One person? Tell me more!
A: In June 1961, Michael Minovitch, a graduate student at UCLA, got a summer job at the Jet Propulsion Laboratory (JPL), where his assignment was to work on an advanced but solvable problem of determining the parameters related to the conic trajectory for a free-fall vehicle passing between two given points and moving within the gravitational field of the Sun (Reference 3).
Q: OK, but that work was not about the gravity assist, was it?
A: Not directly. Minovitch presented his paper on this topic in late July. Working on this problem gave him insight into a far more difficult one which was still unsolved: determining the exact three-dimensional approach trajectory of a free-fall space vehicle approaching a target planet such that the planet’s gravitational field, along with the Sun’s gravitational field, could deflect the vehicle’s unpowered trajectory onto a new path. Known as the “restricted three-body problem” for motion through the solar system, it was one of the most difficult and famous problems of celestial mechanics.
Q: Then what happened?
A: Minovitch believed he could solve this problem by using a different perspective to define a conic orbit in three-dimensional space. By converting from a planet-centered reference frame to a sun-centered reference frame (as he had done for the previous problem), he saw could develop and confirm a new theory for achieving practical interplanetary space travel throughout the entire solar system boosted primarily by gravity-based propulsion.
Q: Was he ignored? After all, he was only a graduate student working on his own time — this was not his formal assignment.
A: Luckily, he was not ignored. He presented his results in late August of that year. Looking at the report today (see the scan of his 41-page paper, Reference 4) is a time-machine trip back to a long-gone world: it was done on a typewriter, the geometric drawings were neatly sketched by hand, and the many special characters (math symbols, Greek letters) were also written in by hand, Figure. It’s closer in style to the elegant, hand-written science and math papers and letters we have from leading thinkers before the 20th century (many of which are now scanned by their various repositories and available online) than to our modern word-processed and PowerPoint presentations.
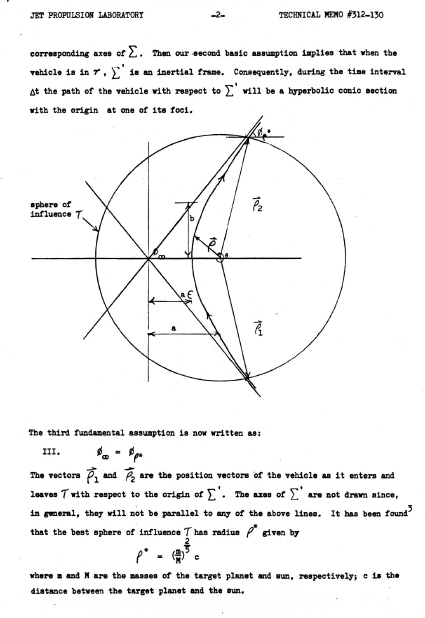
Part 2 of this FAQ looks at how, where, and when Minovitch’s work was applied.
References
- “Gravity assist,” The Planetary Society, https://www.planetary.org/blogs/guest-blogs/2013/20130926-gravity-assist.html
- “A Gravity Assist Primer,” Jet Propulsion Laboratory, https://www2.jpl.nasa.gov/basics/grav/primer.php
- “How Did Minovitch Discover (Create) His New Theory Of Space Travel?,” https://www.gravityassist.com/#_Toc127789952
- Michael Minovitch, “A method for determining interplanetary free-fall reconnaissance trajectories,” Jet Propulsion Laboratory Technical Memo TM-312-130, gravityassist.com/IAF1/Ref.%201-73.pdf, August 1961
- “Voyager: The Interstellar Mission, Mission Overview,” https://voyager.jpl.nasa.gov/mission/index.html
- “Voyager: seeking newer worlds in the third great age of discovery,” Stephen J. Pyne
- “An Introduction to the Mathematics and Methods of Astrodynamics,” Richard H. Battin, American Institute of Aeronautics and Astronautics.





It’s Michael Minovitch throughout, not David Minovitch.
Thank you, Rex. Much appreciated.