Early oscilloscope models were primitive by modern standards. Among the first major innovations was triggered sweep, introduced by Tektronix just in time for the post-World War II electronics boom. This improvement in waveform imaging synchronized successive periodic waveforms to create a coherent image, based on a uniform level along the rising edge or another user-defined benchmark. Digital oscilloscopes were based on Walter LeCroy’s work on high-speed digitizers for the CERN Research Center in Switzerland. Digital oscilloscopes debuted around 1980, supplanting the old analog oscilloscopes. They incorporated a fast analog-to-digital converter (ADC) in conjunction with microprocessors to record, display and manipulate digital waveforms.
Digital scopes also incorporate measurement facilities that can be helpful in making accurate measurements. But the advent of digital scopes also introduced the potential for measurement inaccuracies caused by uninformed selections of scope display parameters. Here we’ll look at some of those difficulties caused by operator decisions about scaling the waveform on the scope display. It turns out that improper display scaling cam make measurements orders of magnitude worse than that at the optimum setting.
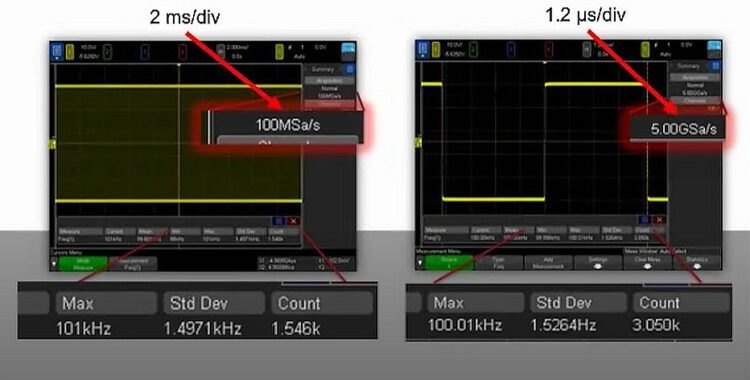
To see the difficulty we will use an example of a 100 kHz clock signal, a frequency low enough that scope bandwidth isn’t a consideration. Many modern scopes incorporate built-in statistical measurement capabilities that can be applied to the signals they display. For this example we’ll use the standard deviation measurement. As a quick review, the standard deviation is a statistical figure of merit showing the spread of measured values around the mean. (In that regard, it’s often used to characterize signal jitter.) The calculation takes a measured value, subtracts the mean, then squares the difference. The scope then computes the average value of the squared differences over the total number of measurements and takes the square root of the average to get the standard deviation.
Suppose we use a scope to validate the 100 kHz signal. For that, we’d set the scope up to make a frequency measurement. Here, the scope might display statistics about the waveform it displays that might include the measured frequency and its standard deviation, and the sample rate at which the scope sampled the signal. A point to note is that the scope sets its sampling rate depending on the length of time needed to reproduce the input, and this time directly relates to the resolution of the time base display.
In the case of a 2 msec/div display resolution the ADC might operate at 100M samples/sec. Further suppose this rate is well below the scope max sampling rate. Now suppose we zoom the time base–and thus reduce the amount of input waveform displayed–to produce a 1.2 μsec/div display. This action can allow the scope sampling rate to rise, perhaps to something like 5G sample/sec.
A further point to note is that the standard deviation measurements of the 100 kHz waveform taken at the two different time base settings is likely to be drastically different–the difference can be on the order of 1,000x. The reason for the smaller standard deviation relates to the scope memory depth, the maximum possible record length for one acquisition. The deeper the memory depth, the higher the sample rate that can be maintained during longer capture time periods.
The key relationship for memory depth MD in scopes is MD = T×S where T = acquisition time and S = sample rate. Scope memory depth is a constant, as is the acquisition time. Thus as the time base is zoomed out, the scope sample rate must adjust to get enough samples to display the waveform over the full acquisition time. Thus zooming in the time base gives a much higher sample rate and, consequently, a frequency measurement with a much smaller standard deviation. Thus horizontal scaling is important for measurement accuracy.
Ditto for vertical scaling. Bits of resolution is the important metric here. As a quick review, the resolution is equal to two raised to the power of the number of bits. As such, an 8-bit converter, as is common on bench scopes, has a resolution of 28 or 256:1. Zooming in on a waveform so it fills the vertical display has a similar affect on the measurement standard deviation as does zooming in the time base. Scaling in optimizes the bits of resolution. Basically a zoom-in makes more quantization levels available for digitizing the waveform of interest. If the waveform of interest doesn’t occupy the whole scope screen, the full resolution of the ADC isn’t being employed. Thus the standard deviation of a measurement that doesn’t occupy the whole screen will likely be larger than that for a measurement where the waveform fills the screen.