There are a variety of possible physical embodiments of quantum computers. This FAQ will explore several of those possibilities. Qubits, Hamiltonians, and decoherence are three important concepts needed when discussing various approaches to quantum computing. Check out the first FAQ in this series for a more detailed discussion of “What are the basics of quantum computing?”
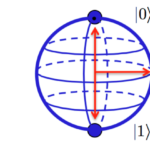
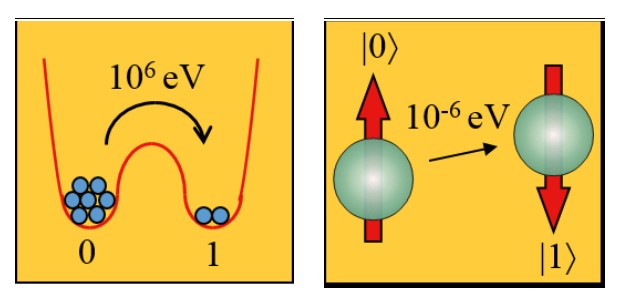
Quantum computing begins with qubits. A classic digital bit can represent either 1 or 0, but not both at once. A qubit is a two-level quantum system where the two basic qubit states are |0⟩ and |1⟩. |0⟩ is the Dirac notation for the quantum state that will always give the result 0 when converted to classical logic by a measurement, and |1⟩ is the state that will always convert to 1. A qubit can be in state |0⟩ or |1⟩, or (unlike a classical bit) in a linear combination of both states.
Classically, two bits can exist in four possible configurations, 00, 01, 10, and 11, but only in one configuration at a time. On the other hand, in a quantum computer, all four possibilities can be encoded simultaneously into the state of the two qubits using superposition of the four quantum basis states |00⟩, |01⟩, |10⟩, and |11⟩. The computation could be executed using a single quantum gate, simultaneously operating on all of the states in parallel.
Quantum decoherence is a major source of errors when working with quantum computers. Any interaction of qubits with the outside environment in ways that disrupt their quantum behavior will result in decoherence. Today’s quantum computers can operate only for concise periods of time (often less than one second, and even good designs only operate for several seconds) before decoherence interferes with their functioning.
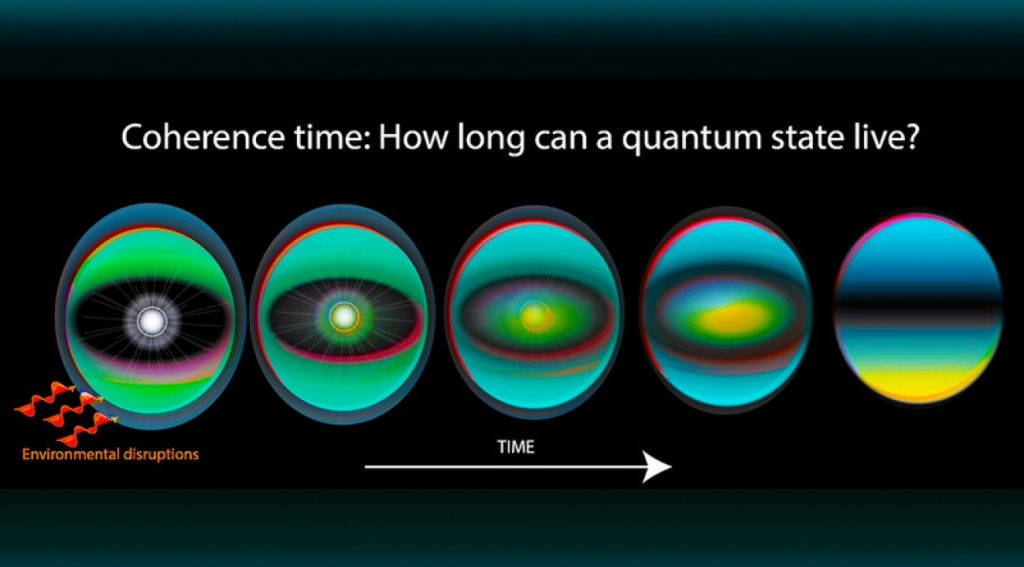
Hamiltonians are also an important aspect of quantum computing. In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of a system. Its spectrum, the system’s energy spectrum, or its set of energy eigenvalues, is the set of possible outcomes obtainable from measuring the system’s total energy.
Encoding a problem as a Hamiltonian energy function applied to the qubits is a common way to implement quantum computing. Typically, the encoding is structured, so the answer reflects the Hamiltonian’s ground state (lowest energy state). This approach results in a series of “energy penalties” that make incorrect answers correspond to higher energy states. Implementation of the corresponding Hamiltonian enables any possible quantum computation to be carried out. Quantum computers can be classified in several ways, one possibility is:
Analog quantum computers (including quantum annealer, adiabatic quantum computers, and direct quantum simulation). These systems operate using coherent manipulation of the qubits, changing the analog values of the Hamiltonian. It does not use quantum gates.
- A quantum annealer operates by initializing the qubits at an arbitrary energy level and slowly changing their energies until the Hamiltonian defines the parameters of the given problem. At that point, the state of the qubits probably corresponds to the answer.
- An adiabatic quantum computer operates by initializing the qubits into the ground state of a starting Hamiltonian and changing the Hamiltonian slowly, allowing the system to remain in the ground state until the Hamiltonian defines the parameters of the problem. As with the quantum annealer, the state of the qubits probably corresponds to the answer at that point.
The challenge for quantum annealers and adiabatic quantum computers is: how slowly is slow enough to change the system? For today’s quantum computers with limited quantum coherence, slow enough may not be possible. Interactions with the environment may disturb the process too much for the computation to be reliable.
Noisy intermediate-scale quantum (NISQ) gate-based computers, sometimes referred to as digital NISQs. Digital NISQs use gate-based operations on a collection of qubits. These systems do not include full quantum error suppression. Therefore, calculations need to be designed to be performed on quantum systems with some noise and be completed in as few steps as possible so that gate errors and decoherence of the qubits don’t obscure the results.
Fully error-corrected gate-based quantum computers. Like NISQs, these are gate-based systems that operate on qubits. Still, these systems are complex and implement quantum error correction to eliminate the negative effects of system noise (including errors introduced by imperfect control signals or device fabrication or unintended coupling of qubits to each other or the environment). These systems enable reductions in error probability rates sufficient that the computer is reliable for all computations. Fully error-corrected gate-based quantum computers are expected to scale to thousands of logical qubits, enabling massive computational capabilities.
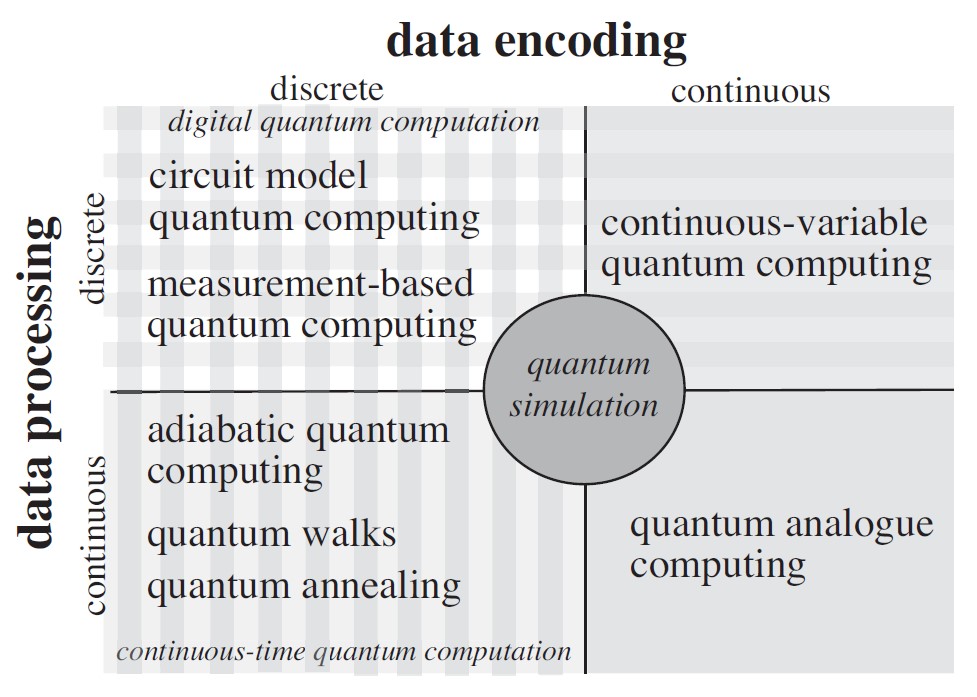
Gate-based quantum computers can have various physical realizations. However, any realizations must satisfy the DiVincenzo criteria:
- A scalable physical system with well-characterized qubits
- The ability to initialize the state of the qubits to a simple quantum state that can be reliably reproduced with low variability
- Long relative decoherence times
- A “universal” set of quantum gates
- A qubit-specific measurement capability
Analog quantum computers need all of the above except for item 4 since they do not use gates to express their algorithms. However, decoherence plays a very different role in analog quantum computing than in the gate model. For example, some decoherence is tolerable in quantum annealing, and some amount of energy relaxation is necessary for quantum annealing to succeed. Quantum computers have been implemented using analog quantum and digital NISQ designs. Fully error-corrected systems are more challenging and are still under development.
Error rate challenges
Error rates and noise are existential challenges for quantum computers. Unwanted variations in energy (noise) are handled differently in classical computers compared with quantum computers. The differences arise from the different characteristics of classical bits and qubits. Classical bits are either zero or one; even if the value is slightly off, separating the signal from the noise and ensuring error-free operation is easy.
However, qubits can be any combination of zero, and one and qubits or quantum gates cannot readily separate and reject noise. Small errors resulting from noise more easily degrade the operation of quantum computers. As a result, isolating quantum computers from all noise sources is an important design criterion, and one of the most important design parameters for quantum computers is their error rate.
The impact of qubit noise sensitivity can be minimized by running a quantum error correction (QEC) algorithm on a physical quantum computer. Without QEC, it is unlikely that a complex quantum program could ever run correctly on a quantum computer. QEC incurs a tradeoff in complexity for lower error rates. Implementation of QES requires large numbers of qubits to form a stable qubit structure called a “logical qubit.” In addition, using a “logical qubit” requires an equally large number of primitive qubit operations to use a logical qubit in a quantum computer effectively.
Toward practical quantum computers
While fully functional quantum computers are still several years in the future, many active development programs are underway to shorten that time. Examples of the quantum computer development efforts underway include Intel and IBM.
Research at Intel Labs has led directly to the development of Tangle Lake, a superconducting quantum processor that incorporates 49 qubits in a package manufactured at Intel’s 300-millimeter fabrication facility in Hillsboro, Oregon. This device represents the third-generation quantum processors produced by Intel, scaling upward from 17 qubits in its predecessor.
In another development activity, Intel is working on perfecting spin qubits that function based on the spin of a single electron in silicon, controlled by microwave pulses. Compared to superconducting qubits, spin qubits far more closely resemble existing semiconductor components operating in silicon, potentially taking advantage of existing fabrication techniques. In addition, this promising area of research holds the potential for advantages in the following areas:
- Operating temperature: Spin qubits require extremely cold operating conditions, but to a lesser degree than superconducting qubits (approximately one-degree kelvin compared to 20 millikelvins).
- Stability and duration: Spin qubits are expected to remain coherent for far longer than superconducting qubits, making it far simpler at the processor level to implement quantum computing algorithms.
- Physical size: Far smaller than superconducting qubits, a billion spin qubits could theoretically fit in one square millimeter of space. In combination with their structural similarity to conventional transistors, this property of spin qubits could be instrumental in scaling quantum computing systems upward to the estimated millions of qubits that will eventually be needed in production systems.
Researchers have developed a spin qubit fabrication flow using Intel’s 300-millimeter process technology that enables the production of small spin-qubit arrays in silicon.
IBM is also wrestling with problems that need to be solved before practical quantum computers can be built. Superconducting quantum computers must deal with the paradox between isolation and access to the qubits. The qubits must be isolated from the environment if they are to realize long coherence. Still, if they are too isolated, the results of the quantum computing process cannot be accessed, making the computer useless. A challenging aspect of developing quantum computers is reading out quantum states with high fidelity in real-time.
IBM has turned to a special class of low-noise microwave amplifiers, known as quantum-limited amplifiers (QLAs), to address this challenge. The performance of QLAs needs improvement before they can support future generations of “large” quantum computers deployed in the cloud. IBM is working to improve the readout fidelity and speed of QLAs and enhance the performance of its quantum chips to improve the synergies between the devices and increase overall quantum computer performance. The next FAQ on “Merging quantum and classical computing in a hybrid system” will dive more deeply into the intersection between classical computing and quantum computing.
Summary
Quantum computing is an emerging area of technology. Multiple possible quantum computer architectures are currently being investigated to identify the best one for specific use cases. Error minimization and correction are major challenges for quantum computing. So are the development of cost-effective and technically feasible qubit structures and solving the paradox between isolation and access of the qubits. Practical large-scale quantum computers are still several years in the future.
References
An Introduction to Quantum Computers Architecture, Researchgate
Quantum Computing – Progress and Prospects, The National Academies of Sciences, Engineering, Medicine
Quantum computing using continuous time evolution, The Royal Society
Reinventing Data Processing with Quantum Computing, Intel
Rising above the noise: quantum-limited amplifiers empower the readout of IBM Quantum systems, IBM
The Strange World of Quantum Physics, National Institutes of Science and Technology (NIST)