Many of the test instruments used in industry today have inputs based on instrumentation amplifiers. This kind of amplifier, sometimes abbreviated as InAmp, is itself based on a more fundamental amplifier setup, the differential amplifier. It can be helpful to understand how these two devices differ.
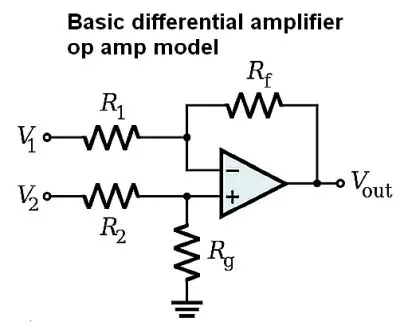 A differential amplifier ideally amplifies the difference two input voltages but suppresses any voltage common to its two inputs. Ideally, differential amplifier output conforms to this equation:
A differential amplifier ideally amplifies the difference two input voltages but suppresses any voltage common to its two inputs. Ideally, differential amplifier output conforms to this equation:
Vout = Ad (V+in – V-in)
Where Ad is the differential gain and V+in and V-in are the two input voltages. In reality, the two inputs on a differential amp have unequal gains. Accordingly, even with inputs that are equal, common-mode rejection is not absolute, and the amp would have an output that is non-zero. Taking this into account the equation for output voltage becomes:
Vout = Ad (V+in – V-in) + Ac ((V+in + V-in)/2)
where Ac is what’s called the amplifier’s common-mode gain.
To eliminate signals (noise, bias voltages, etc.) that appear at both inputs, a low common-mode gain is desirable. It is realized by feeding the amplifier output through an appropriate resistance into the negative input. Most differential amps are based on op-amps these days, and this feedback may be implemented within the op-amp IC or, where temperature rise may be a problem, using a discrete component.
A differential amplifier, to achieve high bandwidth at RF frequencies, must have a single-ended input that matches the source impedance, generally 50 Ω. The InAmp, based around the differential amp, gets around this problem. An InAmp consists of a differential amp with a buffer amplifier on each input. The purpose of the buffer amps is to eliminate the need for an impedance match between the input of the amp and the DUT or whatever is generating the input signal. Additionally, the measuring instrument employing an InAmp input typically has low dc offset, low drift, low noise, high open-loop gain, and a high common-mode rejection ratio.
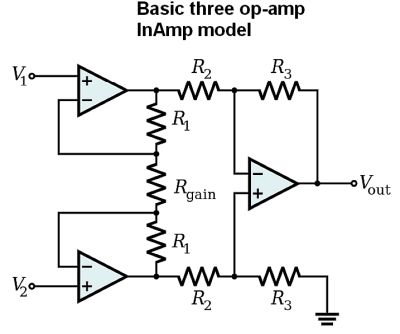 The InAmp is often explained using a model consisting of three op-amps with seven resistors providing negative feedback. Of the three op-amps, one buffers each input. The third is a conventional differential amplifier. The gain is expressed by this equation:
The InAmp is often explained using a model consisting of three op-amps with seven resistors providing negative feedback. Of the three op-amps, one buffers each input. The third is a conventional differential amplifier. The gain is expressed by this equation:
Av = Vout/(V2 – V1 )= (1 + (2R1 / Rgain)) (R3/R2)
where V2 and V1 are input voltages, R3 is the standard feedback resistance for the diff amp, R1 is the feedback resistance for the two unity gain input buffers, and the gain of the differential stage is R3/R2.
The resistor Rgain between the two inverting inputs serves as a way to increase the differential-mode gain of the buffer amps while leaving the common-mode gain equal to one. This increases the common-mode rejection ratio of the circuit and lets the buffer amps handle larger common-mode signals without clipping than would be the case of they were separate and had identical gains. In real-life circuits, Rgain often takes the form of switch-selectable resistors or a potentiometer.
The ideal common-mode gain of an instrumentation amplifier is zero. In the three-op-amp model, common-mode gain comes from mismatch in the resistor ratios and by the mismatch in common-mode gains of the two input op-amps. It can be tough to get resistors to closely match when fabricating these circuits, as is optimizing the common mode performance.
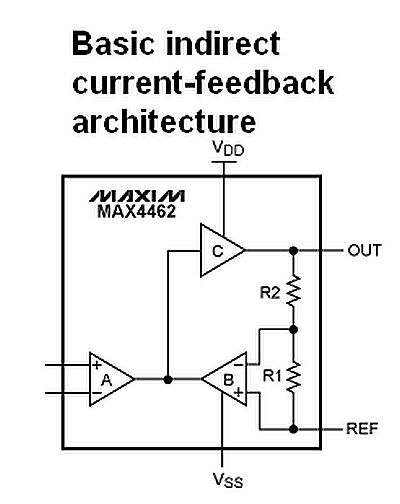
One of the ICs employing the indirect current-feedback architecture is the MAX4462 from Maxim Integrated.
Today most InAmps take the form of a single IC containing the op amps. However, three-op-amp InAmps find only limited application in real-life because of drawbacks associated with the range of common-mode voltages they can work with. A more common InAmp architecture is called indirect current-feedback. The full description of this circuit gets to be quite involved. A simplified explanation is that the circuit contains a high-gain amplifier and two transconductance amplifiers (C, A and B respectively in the nearby schematic). Each transconductance amplifier converts its input differential voltage into an output current and rejects all of its input common-mode voltage. At the stable operating point for the amplifier, the output current sourced from the A stage matches the input current sunk by stage B. This current matching is enabled by feedback action through high-gain amplifier C, which forces the differential voltage at the input of feedback amplifier B to be the same as the differential voltage at the inputs of amplifier A.
This design then sets up a defined current in the output resistor chain (equal to VDIFF/R1), which also flows through R2. Therefore, the output voltage at OUT is simply a gained-up version of the input differential voltage (G = 1 + (R2 / R1)). The output can be offset by feeding an arbitrary reference voltage at REF, much like a standard three-op-amp instrumentation amplifier.
The point to note is that the intermediate signal in the conventional three-op-amp InAmp contains both the amplified differential voltage and also the input common-mode voltage. However, the first stage of the indirect current-feedback architecture provides all the common-mode rejection. The second stage then offers all the differential gain and reinforces common-mode rejection, thereby allowing the output to be offset by a reference voltage, if necessary. Consequently, the input common-mode voltage limitations present in the three-op-amp InAmp just aren’t present in the indirect current-feedback architecture.