A digital signal can be derived from the original time-varying, continuous analog signal by creating a sampled sequence of quantized values. It is intuitively evident that the fidelity and resolution of this quantized signal is based upon the number of samples taken per unit of time. Harry Nyquist published an early version, later further formalized by Claude Shannon, of what has become known as the Nyquist-Shannon theorem, which states that if a system uniformly samples an analog signal at a rate that exceeds the signal’s highest frequency by a factor at least of two, the original analog signal can be perfectly recovered from the discrete version produced by sampling.

Perfectly? Yes, that’s what the theorem says. To comply with the conditions of the theorem, we must recognize that “highest frequency” consists of any and all harmonics, which may be quite extensive. They can be filtered out, but that limits the applicability of the theorem in terms of the bandwidth of the original signal.

However, perhaps surprisingly, there is something to be said for purposely undersampling an analog signal, i.e. using a sampling frequency less than twice the maximum frequency component in the signal. Undersampling is also called band pass sampling, harmonic sampling or super-Nyquist sampling.

The advantages of undersampling arise from the aliasing effect. Suppose a signal F_in is sampled at a rate, F_s, less than twice its maximum frequency. Then the aliased signal appears at F_s – F_in. For example, suppose we sample a 70-MHz signal with 100 MSPS sampling rate. The aliased component will appear at 30 MHz (100 – 70).  The key is that we must know in advance that the signal we see is an alias. We can then recover the actual frequency by using the F_s – F_in relationship.

Use of undersampling employs the ADC as a mixer or a down converter. Undersampling comes in handy for demodulating or extracting information from carrier signals in radio receivers. Consider again a signal of 70 MHz and assume it has a 20-MHz signal bandwidth. If the sampling rate F_s is 100 MSPS, the aliased component will appear between 20 MHz to 40 MHz (30 ±10 MHz).

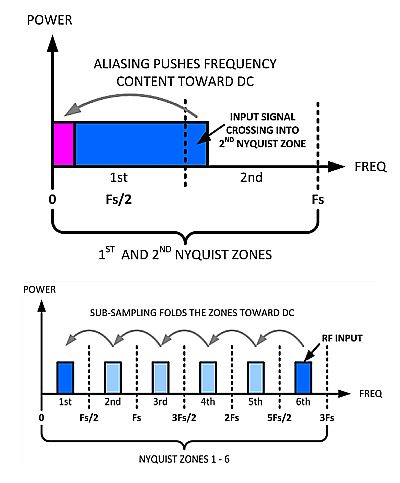
Undersampling uses the concept of what are called Nyquist zones. Nyquist zones subdivide the spectrum into regions spaced uniformly at intervals of F_s/2. Each Nyquist zone contains a copy of the spectrum of the desired signal or a mirror image of it. Odd-numbered Nyquist zones contain exact replicas of the signal spectrum.

Consider once again the 70-MHz signal but assume a 56-MSPS undersampling rate. The 70-MHz signal in this case sits in the third Nyquist Zone and is aliased back in the first Nyquist Zone centered at 14 MHz. A digital down-converter (DDC) can recover this signal for digital frequency mixing that converts it down to baseband and further digital filtering.

Radio designers sometimes use this undersampling technique as a way of eliminating an analog frequency down-conversion stage. The signal alias is not spectrally inverted in this case because it sits in Nyquist zone three, an odd-numbered zone. Even so, spectral inversion can be undone and re-inverted via an FPGA or other means after receiving the data from the ADC. However, spectral inversion does degrade some demodulating processes. Spectral-wise, the inversion is not problematic as long as the spectrum is relatively flat in-band. Also, there may be problems if the entire signal spreads across two Nyquist Zones. Here, the aliased component in the first Nyquist Zone cannot be retrieved by any kind of digital down conversion.

The key advantages of undersampling include the fact that the ADC can consume less power than a version operating at higher frequencies. And the slower ADCs also tend to be less costly. Moreover, it is easier to capture signals with slower ADCs because the set-up and hold times are more relaxed than with those operating at higher speeds. Conversely, undersampled systems employ narrow-band filters that can be challenging to implement depending on the bandwidth and alias frequencies of interest.