by Asem Elshimi, Design Engineer, Silicon Labs
“From a long view of the history of mankind, seen from, say, ten thousand years from now, there can be little doubt that the most significant event of the 19th century will be judged as Maxwell’s discovery of the laws of electrodynamics. The American Civil War will pale into provincial insignificance in comparison with this important scientific event of the same decade.”
― Richard P. Feynman, recipient of the Nobel Prize in Physics in 1965
Electrical engineers tend to dislike hearing about Maxwell’s equations. The equations seem to bring up some frustrating memories to everyone. The conflict starts simply with the way electromagnetism is taught in engineering schools. Lecturers are more often than not flooding the minds of students with a tremendous number of equations and mathematical problems. They keep the students too busy memorizing formulas and solving hypothetical charge problems. Very few engineering lecturers, on the other hand, focus on the underlying physics of such equations or the relevance of such hypothetical problems or developing intuition.

Figure 1. Maxwell equations: Four lines that provide a complete description of light, electricity and magnetism.
Physicists are fond of abstracting concepts into mathematical expressions and operators. On the other hand, we, engineers, we like to understand concepts and feed formulas to computer simulators. The four equations shown in Figure 1 carry an abstract but complete understanding of everything we know about electromagnetism. Professors usually take a few lectures to explain what a field line is and what a differential operator is. But let’s skip this densely mathematical section and jump to what the equations really mean.
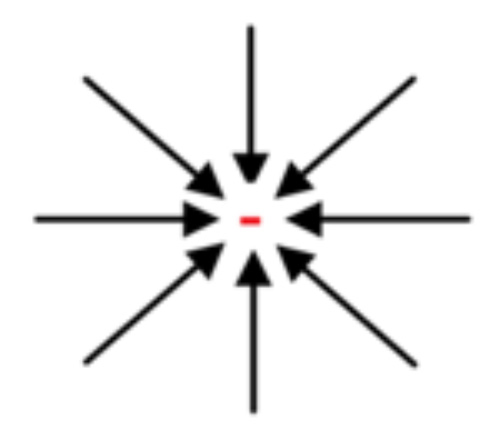 Equation 1 states that electric field (E or D) goes outward/inward (∇.) from an electric charge (ρ). This concept is very simple to grasp. Imagine an electron, and the next thing you see is this electron radiating electric force pulling inwardly and uniformly in all directions. What we mean is that if there was another electron nearby, it would be pushed. We can then use equation 1 in combination with another simple equation that describes how to translate electric or magnetic field into force. Ta-da! We now know how to draw the connection between the amount of electric charge and the amount of force produced.
Equation 1 states that electric field (E or D) goes outward/inward (∇.) from an electric charge (ρ). This concept is very simple to grasp. Imagine an electron, and the next thing you see is this electron radiating electric force pulling inwardly and uniformly in all directions. What we mean is that if there was another electron nearby, it would be pushed. We can then use equation 1 in combination with another simple equation that describes how to translate electric or magnetic field into force. Ta-da! We now know how to draw the connection between the amount of electric charge and the amount of force produced.
Now might be a good time to talk briefly about the term “field.” It is a strange concept. And from personal experience, it is hard to get two engineers to agree on what it actually is. Some think it is a mere mathematical stage that serves in finding out actual forces between objects. And to follow this understanding, we can think of it as an intermediate state of energy that takes place before energy produces forces on objects. So, whenever we talk about fields at a certain point in space and time, we are talking about the possible production of force if an object was to be present at this point of space and time.
 Back to Maxwell’s. Equation 2 states that Magnetic field (B or H) does not flow outward or inward (because the right-hand side is zero). The physical explanation is that the magnetic field is produced by magnetic dipoles. Dipoles are two poles of opposite signs. In other words, there is no such a thing as a magnetic monopole. North and south poles always coexist together. And while the magnetic field produced by the positive side of the magnet would love to traverse the universe outwardly, the negative side of the magnet is always there to pull the field back and causes it only to circulate.
Back to Maxwell’s. Equation 2 states that Magnetic field (B or H) does not flow outward or inward (because the right-hand side is zero). The physical explanation is that the magnetic field is produced by magnetic dipoles. Dipoles are two poles of opposite signs. In other words, there is no such a thing as a magnetic monopole. North and south poles always coexist together. And while the magnetic field produced by the positive side of the magnet would love to traverse the universe outwardly, the negative side of the magnet is always there to pull the field back and causes it only to circulate.
The two equations we described thus far give a complete understanding of electrostatics and magnetostatics. That is, we now know what would happen if the world was at stillness. However, this is not the case. The world is moving, and motion is displacement in space across time intervals. You knew that, didn’t you? So now when electric charges and magnetic dipoles start moving, what is going to happen? Instead of looking at the effects of their movement, we can look at the effect of variations in the fields they produce. Fields are useful in the sense that they help us solve the complete problem by dividing it into two parts. Assume a charge is moved; assume we were able to calculate the fields produced by it; now what are these fields going to do?
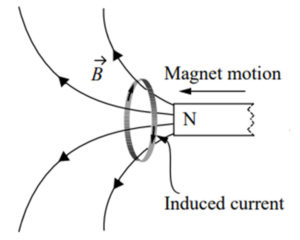 Equation 3 (aka Faraday’s law) tells us that a varying magnetic field (B or H) produces a circularly (∇x) moving electric field (E or D). Faraday discovered this law by bringing a magnet close to a closed-loop wire. His Ameter detected ac current flowing through the circuit. This ac current is simply electrons being pushed around the loop wire by the circularly moving electric field that was produced by the varying magnetic field that came to existence by moving the magnet towards and away from the loop wire. This explains half of the story of what happens inside a transformer. For now, all we know is that if there is a varying magnetic field around a wire, it will create an ac current in the wire. This is what equation 3 tells us.
Equation 3 (aka Faraday’s law) tells us that a varying magnetic field (B or H) produces a circularly (∇x) moving electric field (E or D). Faraday discovered this law by bringing a magnet close to a closed-loop wire. His Ameter detected ac current flowing through the circuit. This ac current is simply electrons being pushed around the loop wire by the circularly moving electric field that was produced by the varying magnetic field that came to existence by moving the magnet towards and away from the loop wire. This explains half of the story of what happens inside a transformer. For now, all we know is that if there is a varying magnetic field around a wire, it will create an ac current in the wire. This is what equation 3 tells us.
Before Maxwell, the world only knew the first half of equation 4 ( ), and this half was known as Ampere’s law. It states that an electric current (J) going through a wire turns this wire into a magnet. And for all we know about magnets, they create magnetic fields (B or H) that flow circularly (∇x). What happens if the current field varies? The magnetic field produced by this current would be inherently variable as well. What if we bring another wire in close proximity to our initial wire? The answer lies in our explanation of equation 3 that took us through what a varying magnetic field can do to a wire. It can generate a circulating electric field in the second wire. We just completed the full story of a transformer.
Now, we are ready to look at what Maxwell added to equation 4. Without going into too much detail, when Maxwell wrote down Ampere’s law, he found out that it is incomplete. In other words, mathematically must equal something more than just J. He did some math to find out the remaining quantity, and it turned out to be the other half of equation 4. This was groundbreaking in the scientific community at the time. Scientists used to write down laws to describe phenomena that they observed. Maxwell was able to derive equation 4 without an initial observation. His input was mathematics. And his output was the description of what was discovered later to be electromagnetic waves.
Maxwell’s discovery was met with strong reluctance from the scientific community. So he wrote letters modeling vacuum as a viscous matter (ether) and went on to explain how his new term makes sense according to his model. While the validity of his model was never confirmed, what really matters is that scientific experimentation only proves his new term to be true. We, unlike scientists of his time, know that what matters is a confirming experiment. Lack of modeling or comprehension of scientific discoveries does not negate their truth… Every empiricist would agree.
Now we are prepared to read equation 4 in its complete “Maxwellian” form: Magnetic field (H or B) can be generated by either electric charges flowing through a wire (J) or varying electric field (D or E.) If we combine this equation with equation 3 (which is what we are about to do), we get to see an electromagnetic wave. Maxwell struggled to explain this phenomenon to his mates. We are so much accustomed to this phenomenon nowadays that we never question how data could be moved wirelessly.
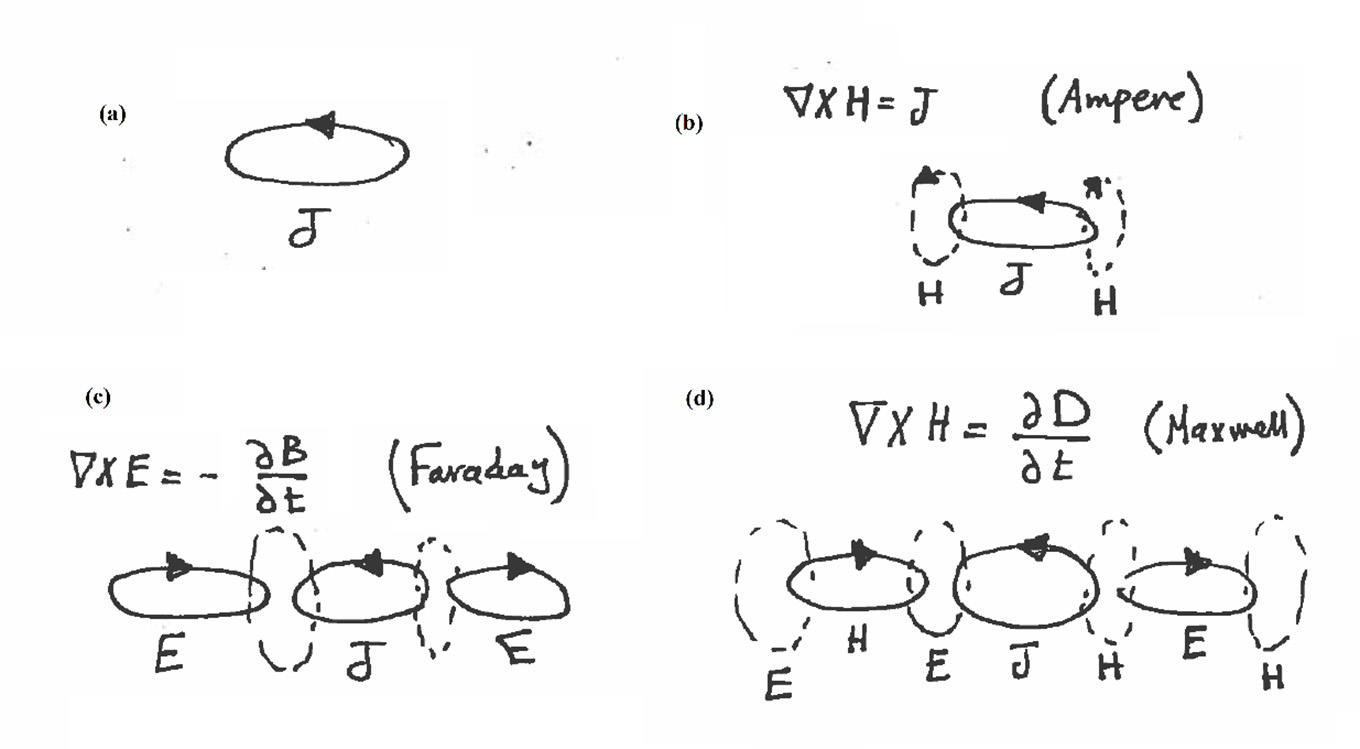
What happens if we have an ac current flowing through a loop wire? According to Ampere’s part of equation 4, a time-varying magnetic field would be flowing circularly around the wire as shown in (a). This time-varying magnetic field, in turn, would like to produce a time-varying electric field. This is what equation 3 tells us. The outermost field shown in (b) is a time-varying electric field. This according to Maxwell’s part of equation 4 means that we can’t help but witness the birth of a time-varying magnetic field, which can, in turn, produce a time-varying electric field. This alternation between the two forms of energy allows electricity and magnetism to traverse space forever. This is how light and heat radiate from the sun to warm and light our world. These are the mechanics by which our cell phones transmit our voice and data out to base-stations.
Up to this point, we have harvested much intuition about Maxwell’s equations without dealing with any of the involved mathematics. The mathematics could be found in textbooks. And if we always look back at the overall picture every time we learn a new equation, the result would potentially lead to a complete understanding of electrodynamics. Whether we need an understanding like this or not becomes a question of what we are trying to accomplish. A good example is solving electric circuit problems. Circuits are fundamentally a bunch of wires and condensers interconnected in a network of nodes. Electromagnetic waves flow through this network and cause the potential to rise through some nodes and currents to flow through some wires.
Based on some assumptions about the size of the circuit and the frequency of operation, Maxwell equations immediately reduce to Kirchhoff Circuit Laws. KCL, for instance, is a combination of Ampere’s law and the law of conservation of charge. If you dare to do the math (which involves converting the four equations of figure 1 into their integral form), you will discover that the sum of currents entering a node equals the sum of currents exiting the node. In short: When we solve circuit problems, we are essentially solving Maxwell’s equations over and over. We are just so lucky that we don’t have to solve them in their complete form. Imagine if we had to design differential low noise amplifiers by solving Maxwell’s at every node. Sigh…
Similarly, if RF engineers are designing a matching network, they are looking at Reflection Coefficient, Smith Chart, and Transmission lines. What they are essentially doing is solving Maxwell’s equations repetitively and interdependently — but again in an abstract form. The well-known set of telegrapher’s equations that lead to the abstract concept of a transmission line are essentially another way to look at equations 1 to 4 combined and manipulated to give quick answers for the electromagnetic fields between a pair of wires.
RF and circuit problems provide an example of what Maxwell equations do. It really goes beyond that. Ask an engineer in a photonics or an optoelectronics lab, and you will find out that the engineering world is currently busy trying to solve Maxwell’s again and again in different geometries and under different conditions. It will only do us better as electrical engineers to appreciate, and hopefully, understand what Maxwell’s equations are all about. We are living in a time when Maxwell’s equations could be solved trillions of times in a very short period using CAD simulators. An intuitive understanding of how fields work would open up possibilities for smarter and more reliable designs.
Acknowledgments: The author would like to thank Dr. John Khoury (Distinguished Engineer at Silicon Labs) for his guidance and feedback.

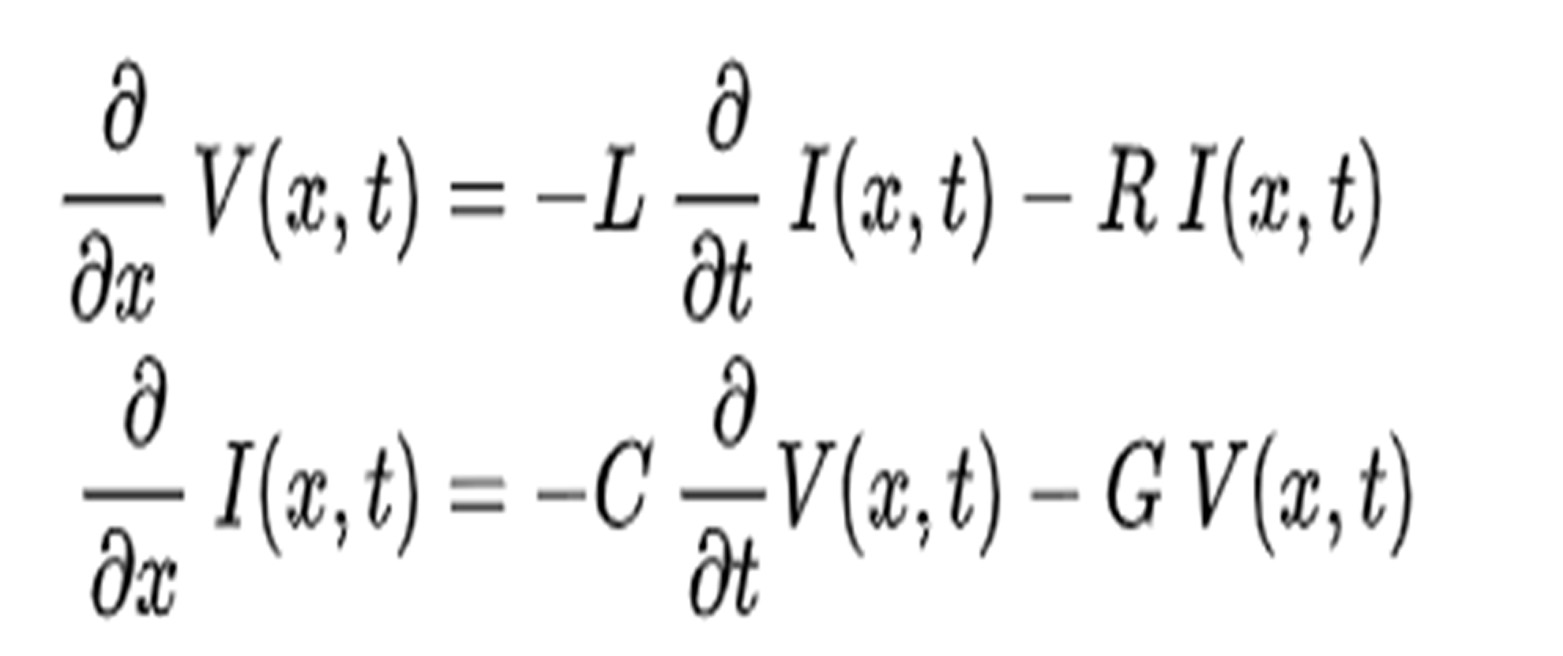

Leave a Reply
You must be logged in to post a comment.