Developing the hardware for quantum computing and hybrid quantum/classical computing systems is only one step in developing practical quantum computing solutions. Development of quantum algorithms and related software programming of the qubits is required to implement practical applications using quantum approaches to computing.
Earlier FAQs in this series looked at the basics of quantum computing, quantum computing system architectures, and the opportunities for merging quantum and classical computing in hybrid systems. This FAQ explores possible applications and some of the algorithms for quantum computing.
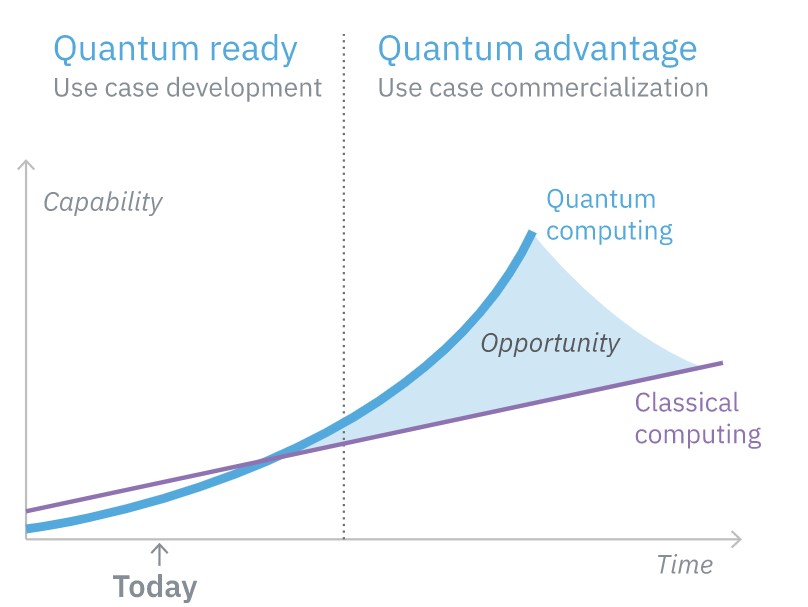
Sometime in the next 10 years, quantum computing is expected to experience widespread commercial adoption. Early adopters are already exploring opportunities to leverage this emerging technology to provide disruptive computing solutions. While not ready for widespread commercial adoption, quantum computing is ready for organizations to explore and prepare for possible use cases and applications so they can enjoy the “quantum advantage” as the technology is rolled out for commercial use.
Cybersecurity
Quantum computing can both enhance and break cybersecurity. The qubits that make up quantum computers cannot be directly observed, and any effort to do so immediately destroys any information that the qubits hold. That could be a boon to enhancing cybersecurity and encryption.
At the same time, quantum computing could be used in the future to break currently used encryption methods. Encryption algorithms such as RSA or SSL/TLS are currently being used to protect sensitive data ranging from passwords to secure transactions and communications. Breaking through that encryption requires such massive amounts of computing power that today’s classical computers can’t do it fast enough to be useful. These encryption schemes are based on prime factorization and the use of huge prime numbers.
Since quantum computers perform multiple calculations simultaneously, they can solve problems beyond the reach of classical computing approaches. And they have the potential to break any conventional encryption system. For example, Shor’s algorithm (discussed in more detail below) could be used to break currently existing encryption schemes. For now, quantum computers are too small and limited in performance to unleash the full potential of Shor’s algorithm. That will change at some point in the future, and cybersecurity, cryptography, and encryption will be fundamentally disrupted. Now is the time to start preparing.
Quantum image processing
Imaging processing provides a good example of the differences between classical and quantum computing. Processes such as image storage, retrieval, processing, noise filtering, and compression can be better performed using quantum approaches to computing. Examples of the differences between quantum image processing and classical image processing include:
- The continuous nature of qubits maps into the continuous nature of image information (color of position data) without pre-processing. For example, the color value of a pixel can be stored or analyzed with qubits using its actual frequency.
- White noise and maintaining high image fidelity can be challenges with classical computing, but they can be simpler to handle in a quantum computer.
- On the other hand, quantum computers can suffer decoherence and lose the entire image. There is a need to balance both types of computing capabilities to get the maximum performance from image processing systems.
- Storing images on a classical computer can lose some relevant information, such as the relationships between various parts of an image in terms of grey-scale values or color temperatures. Quantum computers can store color values (or gray-scale) with more fidelity and corresponding pixel locations of an image using quantum registers.
Problem-solving
The ability to analyze large amounts of data in parallel makes quantum computers especially suited for general business problem-solving. Potential applications range from maximizing the efficiency of transportation or communications networks. And minimization of risk in financial portfolios. Using a classical computer to solve these and similar problems can be problematic. Classical computers can handle only limited data sets, so it’s important to identify the inputs or variables that are most critical.
This is another case where combining the capabilities of quantum and classical computing can improve overall performance. Quantum computers are good at handling multiple variables simultaneously. They can be used to eliminate the unimportant variables and reduce the number of variables to be considered to a set that can be handled by classical computing. Classical computing can then be used to get to a final answer.
Due to their ability to sort through large numbers of possible solutions almost instantly, quantum computers are also expected to be good at solving optimization problems. Airbus is already experimenting with quantum computers to help calculate the most fuel-efficient ascent and descent paths for aircraft. Volkswagen has unveiled a service that calculates the optimal routes for buses and taxis in cities to minimize congestion. And further in the future, quantum computing is expected to provide acceleration for artificial intelligence and machine learning applications.
Pharmaceuticals, medicines, and materials
Pharmaceutical companies expect to use quantum computers to develop better medicines and therapies. Analysis of enzymes and DNA are just two examples. Enzymes are used to catalyze a wide variety of biochemical interactions. Unfortunately, the exact molecular structure of most enzymes is unknown and is unknowable using classical computing. In the future, quantum computing will be used to model enzymes with great precision making it possible to predict specific properties and develop advanced enzymes tailored to produce specific outcomes.
For example, classical computers are challenged to simulate basic chemical molecules with just a few atoms. Proteins are composed of thousands of atoms, making it impossible to model or simulate them with classical computing. As a result, researchers must create and test actual molecules. That’s a time-consuming and expensive process. The ability of quantum computers to accurately and quickly simulate the performance of complex molecules such as proteins and enzymes will reduce the cost and time to market for new medicines.
In addition, therapies for various cancers and other diseases can be improved by a better understanding of DNA. Quantum computing will enable scientists to map DNA in detail, just as classical computing has done for genes.

One of the most promising applications of quantum computers is for simulating the behavior of matter down to the molecular level. Quantum computers are expected to help explore the possibilities of room temperature superconductivity. Auto manufacturers like Volkswagen and Daimler are using quantum computers to simulate the chemical composition of electrical-vehicle batteries to help find new ways to improve their performance. And Cambridge Quantum Computing (CQC) has partnered with the German Aerospace Center (Deutsches Zentrum für Luftund Raumfahrt; DLR) to explore how quantum computing could help create better simulation models for battery development to aid future energy utilization. Quantum computing is also used in simulations to develop improved materials for solar energy systems and wind turbines.

Quantum algorithms
A quantum algorithm is typically a quantum circuit model, often designed to minimize the energy levels of a specific Hamiltonian, designed to solve a specific problem in a step-by-step manner, and that employs quantum phenomena such as quantum superposition and entanglement. A classical algorithm is a finite series of programming instructions for solving a given problem step-by-step.
Because they employ quantum superposition and entanglement, quantum algorithms can solve some problems much faster than classical algorithms. And in some cases, quantum algorithms can solve problems that are beyond the capabilities of classical algorithms. Two of the best-known quantum algorithms are Shor’s algorithm for factoring and Grover’s algorithm for searching an unstructured database or an unordered list. Both have multiple potential applications, including the breaking of cryptographic codes.
Shor’s algorithm for factoring
Shor’s algorithm was invented in 1994 by Peter Shor. It’s a polynomial-time quantum computer algorithm for integer factorization. Given an integer N, Shor’s algorithm finds its prime factors.
In the future, when quantum computers with a sufficient number of qubits can operate without experiencing quantum decoherence, Shor’s algorithm could be used to break public-key cryptography schemes, such as the commonly-used RSA scheme. To implement RSA, a user creates and publishes a public key based on two large prime numbers (which are kept a secret), along with an auxiliary value. Messages can be encrypted by anyone using the public key but can only be decrypted by someone who knows the prime numbers. RSA is successful because factoring large integers is not feasible in real-time using a classical computer.
Shor’s algorithm provides an efficient means for factoring arbitrarily large integers on a sufficiently sized and reliable quantum computer. The existence of Shor’s algorithm is a primary motivation for so-called post-quantum cryptography research into new cryptographic systems that are secure from quantum computers.
Grover’s quantum search algorithm
In 1996, Lov Grover invented a quantum algorithm for unstructured search that has been named Grover’s algorithm. It speeds up unstructured searches quadratically, and it has uses beyond search. It has been used as a general subroutine to achieve quadratic run time improvements for various other algorithms.
Given a large list of N items, one of which has a unique property, such as the key for cryptographic encryption, using a classical computer would require an average of N/2 items, or all N items, in the worst case, to find the one with the unique property. Grover’s algorithm on a quantum computer can identify the item with the unique property in roughly √N steps, a quadratic speedup. And, since the algorithm does not use the list’s internal structure, the algorithm is generic. It can be used to provide a quadratic quantum speed-up for a variety of other classical problems.
Given a sufficiently sized and stable quantum computer, Grover’s algorithm could brute-force a 128-bit symmetric cryptographic key in roughly 264 iterations or a 256-bit key in roughly 2128 iterations. As a result, it is sometimes suggested that symmetric key lengths be doubled to protect against future quantum attacks.
Summary
The hardware needed to support commercial-scale quantum computing is still under development. But, a growing number of efforts are already developing the software infrastructure and algorithms needed to leverage this emerging technology and provide disruptive computing solutions. While not ready for widespread commercial adoption, quantum computing is ready for organizations to explore and prepare for possible use cases and applications so they can enjoy the “quantum advantage” as the technology is rolled out for commercial use.
References
Breaking Cryptosystems With Quantum Computers, Noteworthy
Five strategies to prepare for paradigm-shifting quantum technology, IBM
Grover’s algorithm, Qiskit
Quantum Image Processing — Challenges and Future Research Issues, Arxiv
Shor’s algorithm, Wikipedia