by Hadi Ebrahimi-Darkhaneh, Texas Instruments
A thermistor is a resistive device specifically designed to vary resistance with thermal change, and therefore follows Ohm’s law. According to Ohm’s law, a current passing through a resistive component will produce a voltage drop across that component. This voltage is proportional to the magnitude of the component resistance and the flowing current. Thus, thermistors require an external excitation signal for their biasing and operation, normally with a constant voltage or current source. Although voltage/current sources are designed to be constant, they undergo some variations under different operating and environmental conditions. These variations may cause erroneous readings in temperature measurements.
It is crucial that power-supply interference does not impact actual measurements. Ratiometricity [1,2] is a common approach to negate the effects of power-supply variation. In ratiometricity, the quantity under measurement is proportional to the ratio of two signals rather than to an absolute reference signal [3-6]. In other words, the signal of interest is measured with respect to another signal (such as a voltage or current source) to which it is proportionally related.
This article compares ratiometric and absolute methods in temperature sensing using negative temperature coefficient (NTC) and silicon-based positive temperature coefficient (PTC) thermistors, describing the performance characteristics of the absolute and ratiometric methods through several case studies. Using modeling simulations will determine each measuring system’s performance by revealing system errors.
Figure 1 compares a nonlinear NTC and a silicon-based PTC thermistor in a temperature range from -40°C to 150°C.
Figure 1: Thermistor resistance vs. ambient temperature; the NTC thermistor has large resistance and sensitivity gain at lower temperatures. The PTC thermistor has relatively linear behavior, with roughly constant sensitivity gain.
The Ratiometric Method vs. the Absolute Method
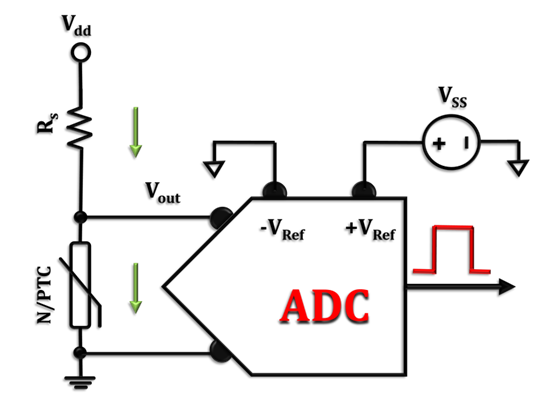
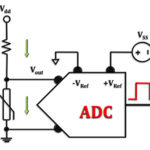
As mentioned previously, power-supply variation is a root cause of measurement errors in thermistors; ratiometricity can negate this effect and improve sensor accuracy. Figures 2 and 3 show two common biasing methods for a thermistor in a temperature sensing network. Figure 2 represents a simplified view of the absolute measurement approach.
Figure 2: Voltage divider network to generate an output signal proportional to the changes in thermistor resistance as a function of temperature; circuit configuration for the absolute temperature measurement method.
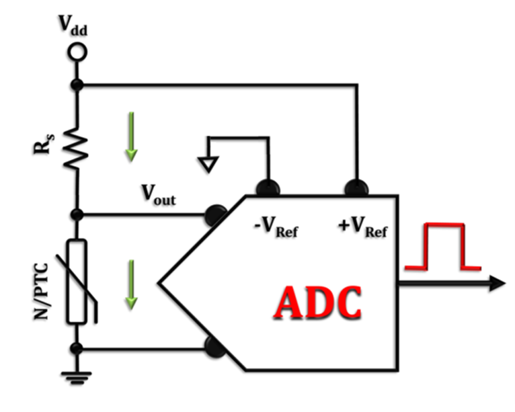
Figure 3 reconfigures the same sensing network for ratiometric measurements.
Figure 3: Voltage divider network to generate an output signal proportional to the changes in thermistor resistance as a function of temperature; temperature sensing using the ratiometric approach.
Corresponding to each method, Equations 1 through 5 describe the relationship between the different circuit components of Figures 2 and 3 and the analog-to-digital (ADC) output result. These equations also describe the relationship between the divider network output signal and the ADC’s output result.
In Equation 1, N denotes the ADC’s resolution bit, and Vss is the independent reference voltage:
Equation 2 expresses the temperature-dependent signal across the thermistor (Vout):
Substituting Vout in Equation 1 with the actual term given by Equation 2 yields Equation 3:
From Equation 1, you can see that the measurement accuracy of the absolute method (Figure 2) is susceptible to external variations and thermal drifts from three different sources: Rs, Vdd and Vss.
In the ratiometric approach shown in Figure 3, the reference voltage is picked from the main supply voltage (Vdd) instead of using an independent external voltage source (Vss). Assuming that the wires connecting Vdd to the reference input and ground terminals (±Vref) have a minimal impedance effect, Equation 4 expresses the reference voltage of the ADC as:
Substituting the new reference voltage from Equation 4 into Equation 3, Equation 5 simplifies the ADC output result:
Equation 5 shows how the ratiometric technique completely illuminates the dependency of the ADC output result on the Vdd and Vss voltage sources.
Case 1: The Absolute Method
The core of the study in this section is to characterize system performance using the absolute measurement approach. To verify measurement accuracy, three nonideal components are used for Vdd, Vss and the current-limiting resistance (Rs), assuming that:
- The supply voltage has some ±DC offset proportional to the nominal value of the voltage source.
- The supply voltage has some dependency on the ambient temperature, in which the voltage drift is given by a constant (negative) temperature coefficient.
- Similar to the voltage source, Rs also has some fixed tolerance, as well as a PTC to describe the actual behavior of Rs under different ambient temperatures [4,5].
Although in a practical situation these components may show somewhat nonlinear behavior, for simplicity I have only considered linear variations. Equations 6, 7 and 8 are the mathematical models describing each component’s dynamics.
In Equation 6, the Rs resistor from different vendors comes with a ±max tolerance (as a percentage of the device’s nominal value) and a temperature coefficient. All of these parameters can be easily found in the device’s data sheet or other supporting documents.
Equations 7 and 8 express the common behavior seen in most nonideal power supplies and voltage regulators:
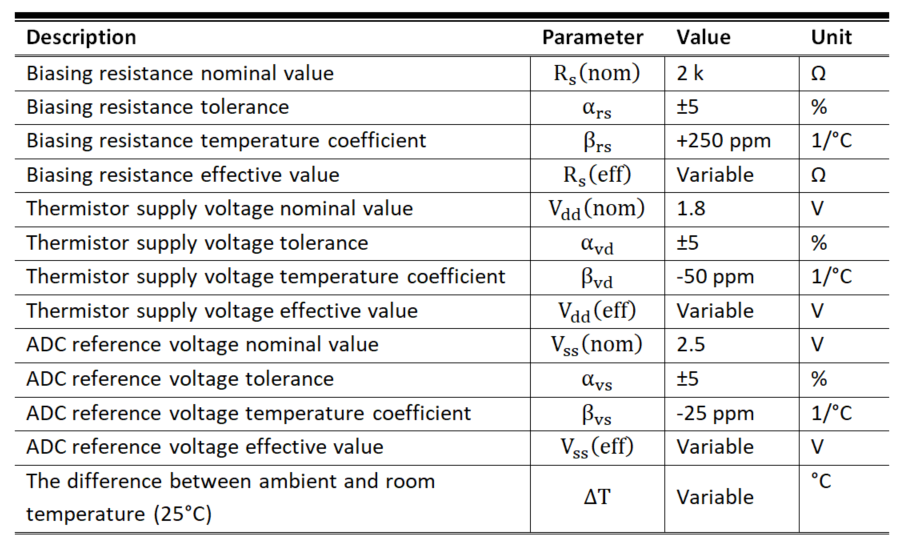
Table 1 lists the parameters used for the modeling simulations.
Table 1 lists the parameters used for the modeling simulations.
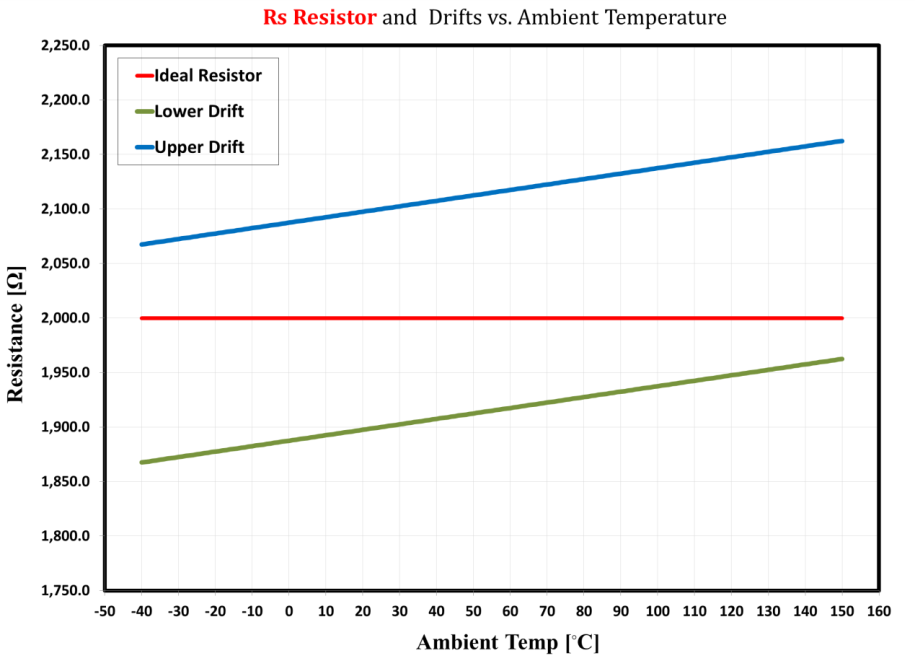
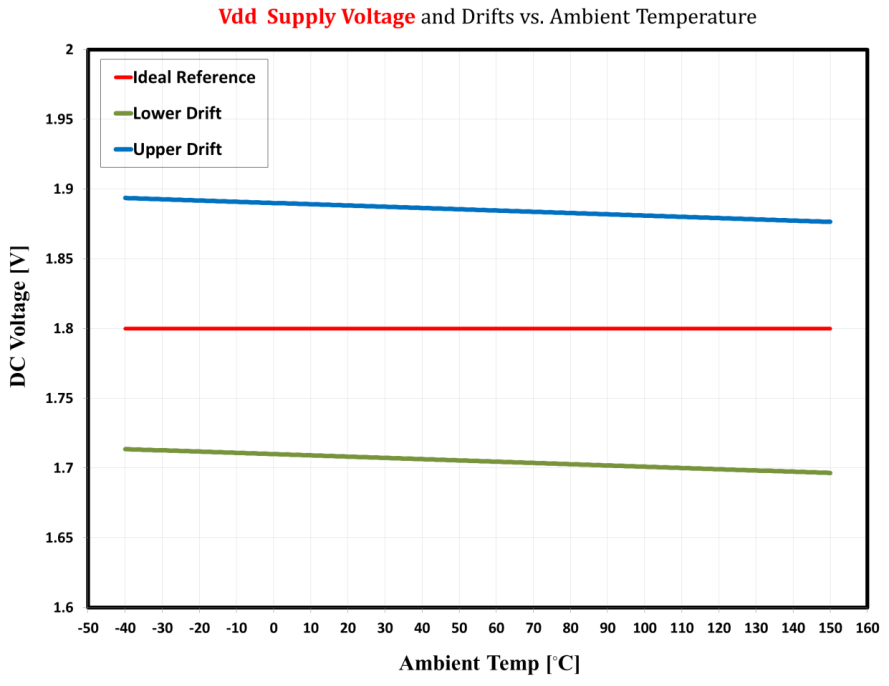
Figure 4 compares the ideal resistor component (Rs) and the actual values caused by variations discussed above. Figures 5 and 6 provide similar comparisons for the thermistor biasing voltage (Vdd) and the ADC’s reference voltage (Vss). These deviations from the nominal values can substantially affect sensor measurement accuracy, as shown in Figures 6 and 7.
Figure 4: Performance characteristics of the current-limiting resistor (Rs) used for the modeling simulations. The nominal value for this resistor is 2 kΩ, with a ±5% factory tolerance and 250-ppm temperature drift.
Figure 5: The ideal vs. actual supply voltage at different ambient temperatures. The supply-voltage variation is due to the ±5% DC offset plus a -50-ppm temperature drift.
Figure 6: The ADC reference voltage profile vs. the ambient temperature. Deviation from the ideal value is the result of the ±5% DC offset plus a -25-ppm temperature drift.
Given these component tolerances, let’s see how these variations affect temperature accuracy performance. As a reminder, there are three components with nonideal profiles; Vdd, Vss and Rs. For each individual component, there were three possible behaviors displayed in Figures 4, 5 and 6. Therefore, the total number of possible system errors is 3 × 3 × 3 = 27.
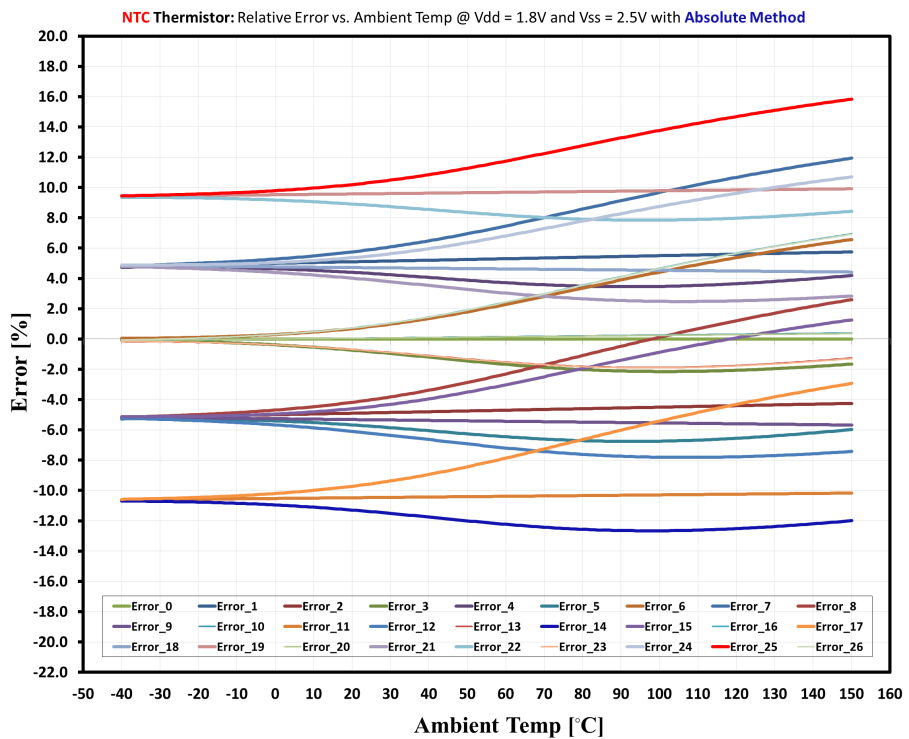
Among all possible solutions out of these 27 cases, there is only one case that returns zero measurement error. Of course, that is the best-case scenario in which all of the components are ideal. For the remaining cases, a nonideal component response would cause an erroneous sensor reading. Figure 7 shows the measuring system error due to all possible component variations.
Figure 7: Measuring system errors caused by Rs, Vdd and Vss components with an NTC thermistor, based on simulation results for all 27 scenarios for an ambient temperature range from -40°C to 150°C
Figure 7 also indicates the nonlinear error profile vs. the ambient temperature. This nonlinearity is attributed to the nonlinear nature of an NTC thermistor.
The error results for this study are generated using the ADC output signal given by Equation 9:
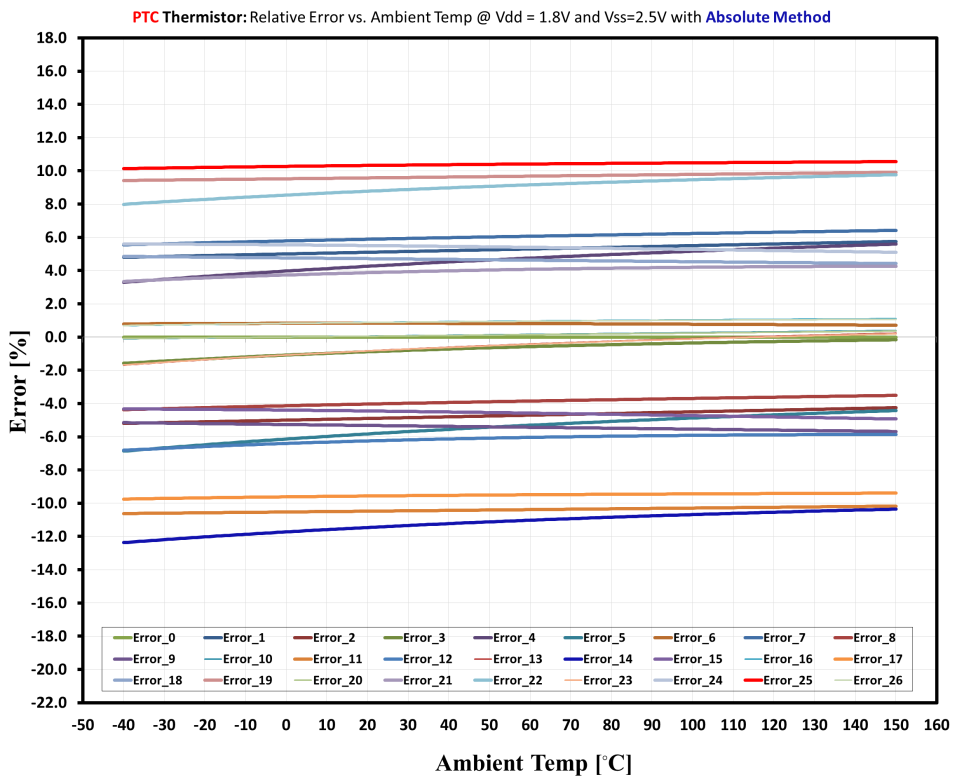
Figure 8 includes the simulation results taken for the absolute method using a silicon-based PTC thermistor. The process is identical, except that a PTC thermistor replaces the NTC thermistor. From Figure 8, you can see that the error profile shows a roughly linear response, attributable to the unique properties of the linear PTC shown in Figure 1.
Figure 8: Measuring system errors taken for all 27 cases with a silicon-based PTC thermistor, based on simulation results for an ambient temperature range from -40°C to 150°C. There are more flat responses compared to an NTC thermistor.
Case 2: The Ratiometric Method
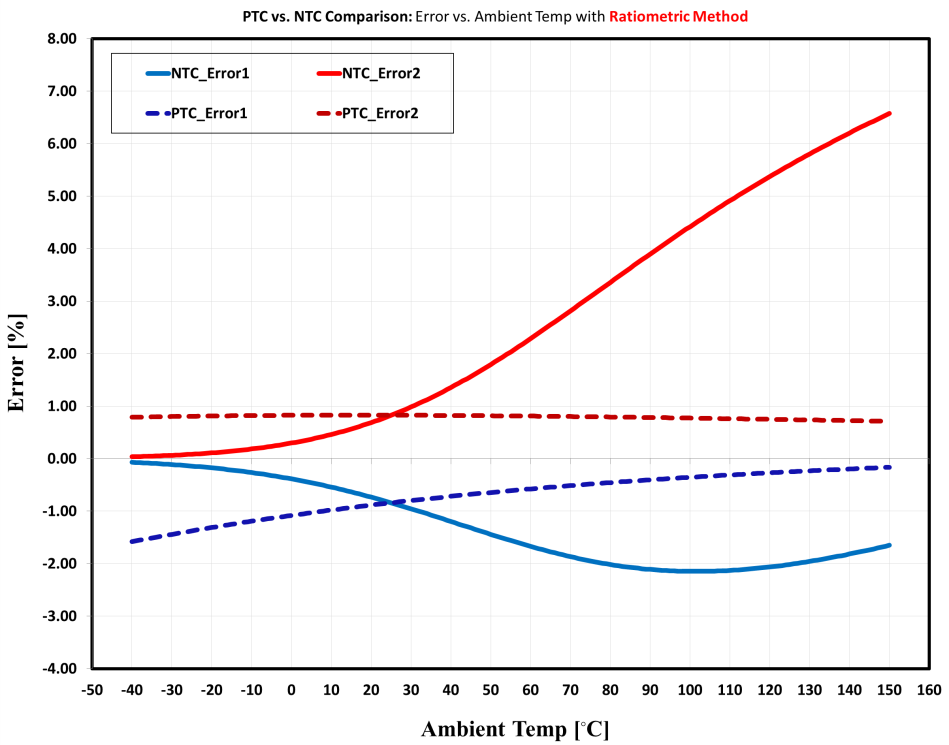
Let’s examine the performance of the measurement system when using the ratiometric method. The circuit configuration in Figure 3 characterizes system errors using the same NTC and PTC thermistors, like Case 1. Remember from Equation 5 that the ADC output signal is now only susceptible to biasing resistance (Rs) variations. As a result, the number of possible scenarios caused by component variations has declined substantially: 27 possible error cases in the absolute method compared to two in the ratiometric method. Figure 9 shows the simulation results captured for temperature measurement errors using the ratiometric approach. Comparing the results of Figure 9 with those of Figures 7 and 8 show that the ratiometric technique produces much lower errors compared to the absolute method. Figure 9 also compares the measuring system’s relative error using the NTC thermistor and the silicon-based PTC thermistor given by Figure 1.
As Figure 9 illustrates, the error percentage obtained for the NTC component is showing slightly better performance for the lower temperature range. However, at around room temperature and above, the PTC error percentage is much less. The results obtained for the linear PTC are also showing a somewhat flat response, much like the case with the absolute method. This can be a great argument for using linear PTC sensors for cost-effective calibration, such as single-point calibration.
Figure 9: Measurement errors obtained for PTC and NTC thermistors using the ratiometric technique. The linear PTC thermistor had a lower measurement error.
Conclusion
The ratiometric technique can be quite effective in rejecting external turbulences and improving system measurement accuracy. The ratiometric method also circumvents the need to use an additional supply voltage, which may add to system complexity and cost.
The simulation results demonstrated that the silicon-based PTC would result in much better performance in terms of precision and predictability. Contrarily, the use of a nonlinear NTC can lead to erroneous readings and poor measurement accuracy. Therefore, the combination of the ratiometric method and a silicon-based PTC may be the best solution for temperature sensing.
For more information on linear PTC thermistors, see https://www.ti.com/product/TMP61.
References
- White paper: Voltage measurement accuracy, self-calibration, and ratiometric measurements
- White paper: Low power programmable temperature controller
- Analog Applications Journal: Ratiometric measurements in the context of LVDT-sensor signal conditioning
- Application report: Effect of resistor tolerances on power supply accuracy
- EDN: Worst-case circuit design includes component tolerances
- Journal of Atmospheric and Oceanic Technology: Sensor and electronic biases/errors in air temperature measurements in common weather station networks


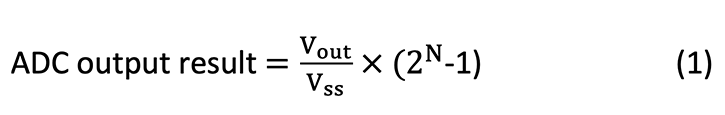
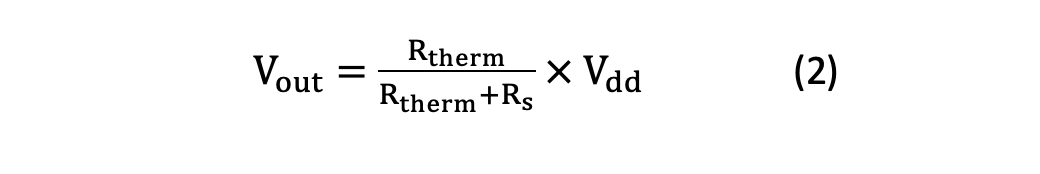

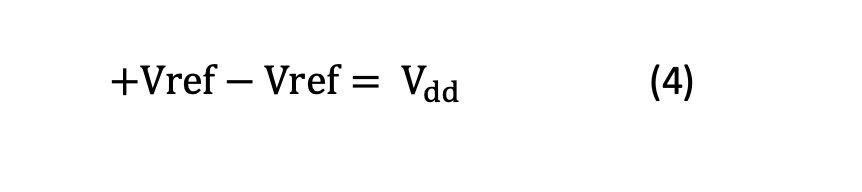

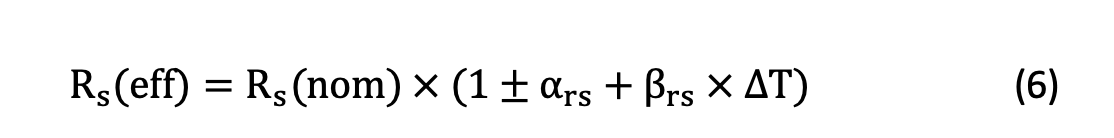
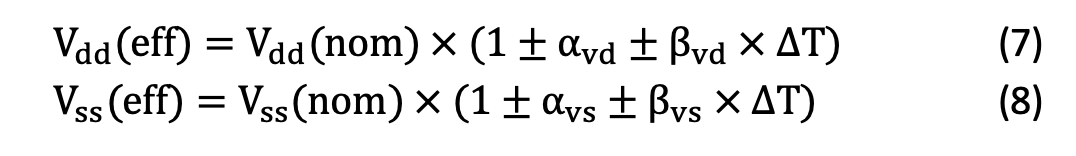
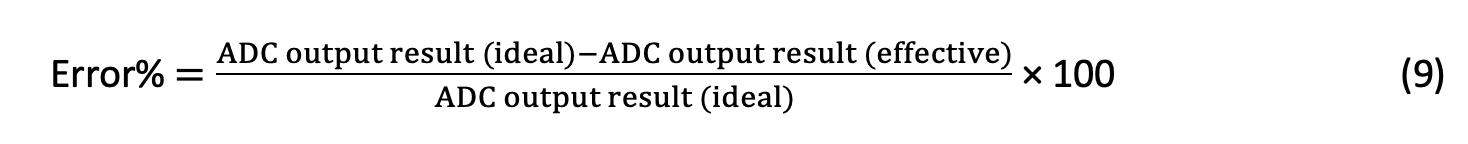




Leave a Reply
You must be logged in to post a comment.