Can I park in one of your Lagrange points?: Part 1

Analysis and insight from an 18th-century mathematician were used to place the James Webb Space Telescope in a “parking spot” optimally suited for its imaging, communication, and solar-power needs.

You’ve undoubtedly followed the stunning success of the James Webb Space Telescope (JWST), launched in December 2021 (Figure 1). It is now about 1.5 million kilometers (1 million miles) away from the Earth at what is called the second Lagrange point or L2, looking “back in time” to the furthest reaches of the universe with imaging systems in multiple, mostly infrared optical-spectrum bands.

Fig 1: Artist’s conception of the James Webb Space Telescope with its solar panels and shield fully deployed. (Image: NASA)

There are so many fascinating aspects from design, engineering, validation/test, and other standpoints, beginning with its multipaneled mirror array, custom A/D converters, multiple power sources and subsystems, on-board cooling (6.4 kelvins), various communication links, and more… it’s a very long list.

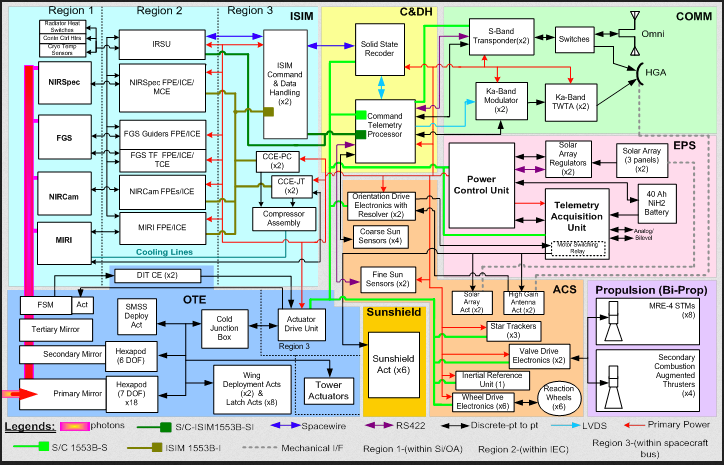
Even a high-level block diagram cannot begin to show the complexity of this design and the relationships amount its many pieces (Figure 2). Yes, this collaboration among NASA, the European Space Agency (ESA), and the Canadian Space Agency (CSA) was about a decade behind schedule and billions of dollars over budget—but how do you even begin to work out a schedule and budget for such a complicated project with its countless design and implementation unknowns?

Fig 2: This “big picture” block diagram of the many functional blocks of the JWST cannot even begin to show the system’s actual complexity and introduces many unfamiliar acronyms. (Image: NASA)

One aspect of the JWST that fascinates me is where the JWST is sited in space because it builds on mathematical work done back in the 1700s by Italian-French mathematician Joseph-Louis Lagrange (born Giuseppe Luigi Lagrancia) and many of his contemporaries. (Lagrange was prolific: he published several hundred papers!)

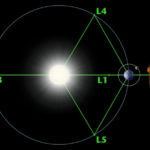
The JWST is “parked” (we use that term loosely) at one of the five Lagrange points, which exist around two other bodies attracted to each other by gravitational forces. Obviously, Lagrange had no idea that his analytical insight would be used to place an observation satellite in space.

Lagrange’s points and the three-body problem

The context for the three-body problem is this: the orbits and motions of two bodies in isolation can be worked out exactly and analytically. But by Lagrange’s time, it was known that the situation was different for the three-body problem. This involves taking the initial positions and velocities of three masses and solving for their subsequent motion according to Newton’s laws of motion and Newton’s law of universal gravitation.

Unlike two-body problems, no general closed-form solution exists, so the solution requires numerical methods using calculations rather than closed-form equations. This insight extends to the more general and also unsolvable case of the n-body problem, which affects the analysis of motions of planets around our Sun, for example.

The three-body problem is quite common; historically, the first specific three-body problem to receive extended study was the obvious one involving the Moon, Earth, and the Sun, of course. Although the general case of the three-body problem could not be solved analytically, it was also shown that if the ratios of masses among the three bodies met some specific criteria, the equations could be simplified to yield an analytical solution in closed form.

Lagrange worked on this problem during an era when mathematicians (many of whom were also astronomers or broad-interest scientists) would identify and present problems and challenges to each other or publicize ones that they had already solved. Keep in mind that this was a time when all contact was by slow mail, so communication and cooperation were lengthy.

Lagrange identified five special points where a small mass can orbit in a constant pattern with two larger masses (Figure 3). These are positions where the gravitational pull of two large masses precisely equals the centripetal force required for a small object to move with them. Lagrange considered this mathematical problem, known as the “General Three-Body Problem” in his prize-winning paper (Essai sur le Probleme des Trois Corps, 1772).

Fig 3: Lagrange analyzed the behavior of three bodies moving around the center of mass over elliptic orbits and solutions to the resultant equations. (Image: ResearchGate)

There’s no need to go through his analysis and equations here. If you are interested, there are many good online presentations, of course (see References). If you are ambitious, you can even try to read Lagrange’s approximately 100-page paper in its original French translation, but note that the nomenclature, designations, and even sentence structure used in the 1700s differ significantly from what we use today. ( I have not yet found an English translation of his paper.)

The second part of this article looks at the relationship between the Lagrange points and space observations.

EE World Related Content

Reaction wheels ensure satellites maintain the right attitude: Part 2
Now that’s a test instrument: Inside the Webb space telescope
Testing On the James Webb Space Telescope
The Hubble Space Telescope: Part 4

External References

JWST and Lagrange Points