Analysis and insight from an 18th-century mathematician were used to place the James Webb Space Telescope in a “parking spot” optimally suited for its imaging, communication, and solar-power needs.
There’s more to the n-body story and Lagrange’s work. All planets orbit the Sun in an oval, as characterized by Kepler’s Laws, so there is a point in that orbit called the perihelion that is closest to the Sun.
For hundreds of years, astronomers were puzzled by an inexplicable aberration in the orbit of Mercury. They observed that as Mercury orbits the Sun, its perihelion advances by a small amount, and Newton’s theory does not fully explain this precession of Mercury’s perihelion (Figure 1).
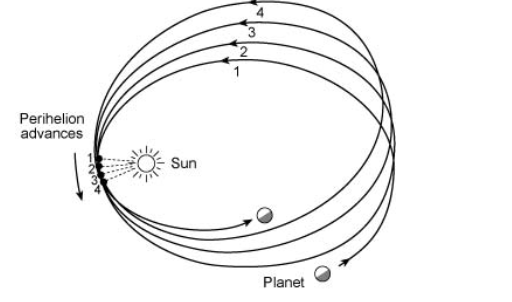
The discrepancy between the Newtonian prediction, which results from the gravitational tugs of the other planets, and the observed precession is tiny—just 43 arcseconds per century—yet astronomers hundreds of years ago were able to measure this with their “crude” instruments (certainly crude by our standards), do the calculations, and note and puzzle about the difference. This tiny difference could not be explained, even after accounting for the effect of the gravity of the Sun and other planets using n-body theory and mathematical analysis. Some astronomers even theorized that there was an unknown planet inside the orbit of Mercury (called Vulcan) which could account for the odd behavior of Mercury.
Once again, Einstein’s general theory of relativity provided an explanation. He showed that the aberration is because the gravitation forces on Mercury are being “distorted” by the curvature of spacetime. Working with the orbital numbers and then making accommodations for relativistic effects, Einstein accurately calculated the amount of perihelion shift that should be observed—and which was—and so resolved the long-standing dilemma.
More on Lagrange: his multiplier
While Lagrange is known for his work on the three-body problem, his work also extended to other areas. He developed what is known called the Lagrange multiplier technique, now widely used in optimization analysis. This technique lets you find the maximum or minimum of a multivariable function f(x, y, …) when there is some constraint on the input values you are allowed to use. This is a common situation that is generally very difficult to resolve analytically.
For example, you may want to maximize the function f(x,y) = 2x + y while also subject to the constraint that x2 + y2 = 1. In the Lagrange multiplier approach, you convert this constrained problem into another unconstrained form and determine the derivatives of an unconstrained problem. The relationship between the function’s gradient and the constraints’ gradients leads to a reformulation of the original problem, known as the Lagrangian function, which can then be used to analyze and solve the problem. Despite the complexity of the technique, it is often used in the case of the constrained optimization problem.
It may seem an anomaly that an abstract three-body problem worked on in the 1700s has been applied to the siting of the JWST and other satellites, but this is not the case at all. In fact, much of today’s astrodynamics uses work done in those “ancient” days, which long predate calculators, computers, email, and our other modern tools.
If you have any doubts about this, look through “An Introduction to the Mathematics and Methods of Astrodynamics” by Prof. Richard H. Battin (Figure 2). This classic, still widely used 1968 work by Battin—a senior MIT professor and lead member of the staff of the Charles Stark Draper Lab—includes the essential elements of celestial mechanics, spacecraft trajectories, and space navigation.

Keep in mind that whenever you talk about astrodynamics—the study of the motion of natural and artificial bodies in space, based on Newton’s Laws of Motion and his law of universal gravitation—there are a few points to keep in mind. First, there is no such thing as traveling in a straight, every path is curved, and even perfectly circular orbits don’t exist. Second, there is no such thing as a motionless object, only motion (or lack thereof) with respect to some defined frame or body of reference.
Battin and his team developed the guidance analysis and calculations for the Apollo mission, and the book shows the complexity of the astrodynamics math needed to work out orbital and Earth-moon trajectories. It’s especially complicated because, in most cases, you need the “aim” to be almost 100% right the first time, as there is only a limited opportunity (time, fuel, and other resources) for anything other than minor course corrections. He further points out that “the object is not simply to hit a target…on the contrary, the Apollo vehicle must miss the moon by a carefully controlled amount.” That perceptive insight overshadows and affects the entire navigation and guidance process.
Battin not only goes through the extremely sophisticated equations and their historical context but also shows where they can be simplified under specific circumstances to make them manageable. He often cites specific advances of mathematicians and astronomers such as Newton, Euler, Kepler, Laplace, Descartes, Hooke, and others for their works in framing problems, exploring solution paths, discussing the implications, and showing ways to resolve what seem to be intractable issues or prove that they can’t be solved analytically.
While the book is technically intense, his introduction is a model of non-academic clarity and insight into the multiple inherent problems faced by the discipline of astrodynamics and the general paths to solutions, as well as provides fascinating historical context. Even if the remainder of Battin’s technical discussion is “over your head,” his frequent references to the insight provided by those predecessors give perspective and depth to Newton’s famous statement (In a letter to Robert Hooke in 1675), where he wrote: “If I have seen further it is by standing on the shoulders of giants.”
EE World Related Content
Reaction wheels ensure satellites maintain the right attitude: Part 2
Now that’s a test instrument: Inside the Webb space telescope
Testing On the James Webb Space Telescope
The Hubble Space Telescope: Part 4
External References
JWST and Lagrange Points
- European Space Agency, “James Webb Space Telescope”
- NASA, “L2 Will be the James Webb Space Telescope’s Home in Space”
- NASA, “What is a Lagrange Point?”
- NASA, “The Lagrange Points” (Detailed mathematical analysis)
- European Space Agency, “What are Lagrange points?”
Three-body problem
- Joseph-Louis Lagrange, “Essai sur le Probleme des Trois Corps” (scan of his original published paper)
- Ellis Strömgren, Translation of the paper “Connaissance actuelle des orbites dans le problème des trois corps” or “Current knowledge of orbits in the three body problem” (an early 20th-century paper which is a modern update on Lagrange’s work)
- Sylvio R. Bistafa, University of Sao Paulo, “Euler’s three-body problem”
- Scholarpedia, “Three body problem”
Mercury perihelion and precession anomaly
- NASA, “Newtonian gravity and Einstein’s Theory of General Relativity”
- Wikipedia, “Test of General Relativity”
Lagrange Multipliers
- Machine Language Mastery, “A Gentle Introduction To Method Of Lagrange Multipliers”
- Khan Academy, “Lagrange multipliers, introduction”
- Wikipedia, “Lagrange Multiplier”



Leave a Reply
You must be logged in to post a comment.